Haskell | Monad初探
摘要:学习Haskell的过程中一时无法理解Monad的概念,于是探索了一番,将心得记录如下。
我试图从如下的定义里看穿Monad的真相。
A monad in X is just a monoid in the category of endofunctors of X, with product × replaced by composition of endofunctors and unit set by the identity endofunctor.
Monad是自函子范畴上的幺半群。
概念解释
首先,对于如下相关的概念我尝试给出我自己的定义。
类型系统
Haskell的类型系统相当复杂。不同于OO只是一层抽象,Haskell抽象多得可怕。目前我给出的分层如下:

从下往上是按照从具体到抽象。首先是具体的值Value,其次是将Value抽象为特定类型Proper Type,然后Proper Type又被抽象为高阶(包含一阶)类型Higher Order Type,最后是最抽象的kind。而Monad是什么呢?它是kind为* -> *的一种类型类。
函数与函子
此处的函数狭义地仅指Haskell里的方法,即输入参数和输出参数均为
Proper Type的一一映射
函数Function是指输入参数和输出参数均为Proper Type的一一映射,而函子Functor是指输入参数和输出参数均为Higher Order Type的一一映射。其中Functor的定义不够准确,在范畴部分会继续补充。
自函数与自函子
前面我们已经给出了Function的定义,用代码表示就是Type A -> Type B。如果此处的Type B包含于Type A,那么我们就称此函数为自函数Endofunction。特别的,如果Type B等于Type A,则称其为Identity Function。
类比自函数,什么是自函子Endofunctor呢?对于Higher Order Type A -> Higher Order Type B,如果Higher Order Type B包含于Higher Order Type A,则我们称此函子为自函子。同样的,如果Higher Order Type B等于Higher Order Type A,则称其为Identity Functor。
范畴
我不打算从很严谨的定义阐明范畴Category的概念。通俗地讲,我理解的范畴就是对象+态射。那么在Haskell中什么是范畴呢?
最重要的我认为是一个Higher Order Type对应于一个Category,其中被该Higher Order Type所抽象的Proper Type就是该Category的对象,而以这些Proper Type为入参和出参的Function就是该Category的态射。
函子深入
然后Functor的概念可以进一步深入。刚刚说道,函子Functor是指输入参数和输出参数均为Higher Order Type的一一映射,更准确的,Functor是Higher Order Type所对应的范畴之间的映射,它包括对对象的映射和对态射的映射。举个例子,考虑a -> [a]作为Functor,它是Identity对应的范畴和List对应的范畴之间的映射。第一它可以作为对象之间的映射,例如它是Int -> [Int]之间的映射,第二,作为对态射的映射,由于[]有map方法,所以它还是(Int -> Int) -> [Int] -> [Int]之间的映射。
在Haskell中有类型类
Functor,它接受高阶类型作为实例,高阶类型本身就是类型构造器,它就是对象之间的映射。Functor实例必须实现fmap方法,它又是态射之间的映射。
半群与幺半群
我们知道群是指满足的封闭性、结合律、有幺元、逆元的非空集合+二元运算(G, *)。当(G, *)满足封闭性、结合律时它是一个半群,进一步,如果还有幺元,则它是一个幺半群。
Monad
上面说了一大堆,如果不具体到Monad的定义上被觉得都是扯淡。回顾开头部分引用的定义。
Monad是自函子范畴上的幺半群。
自函子范畴
首先,考虑什么是自函子范畴?上面说过,粗浅地认为范畴=对象+态射。既然是自函子范畴,对象自然是自函子。而实际上如果把Haskell所有类型和方法统一作为一个范畴,则Haskell上所有的函子都是自函子(这一点还有些模糊)。用Haskell代码表示这里的自函子就是a -> m b,其中a, b是类型参数,m是高阶类型。
那么接下来的问题就是自函子范畴上的态射是什么。根据函子范畴的定义,这里的态射叫做自然变换。维基上的解释还比较清晰,用Haskell代码表示从函子a - > m b到a -> m c的自然变换就是m b -> m c。所有这些自然变换就构成了自函子范畴上的态射。
自函子范畴上的幺半群
然后作为这个自函子范畴上的幺半群(G, *),非空集合G自然就是自函子构成的集合,而二元运算*是什么呢?幺元是什么呢?
回忆Haskell中对Monad实例的要求是实现return函数和>>=函数,它们的定义如下:
class Monad (m :: * -> *) where
(>>=) :: m a -> (a -> m b) -> m b
return :: a -> m a
根据函数声明可以看出,return本身就是一个特殊的自函子,而>>=酷似二元运算。我们自然地猜测>>=就是这个幺半群的二元运算,reutrn就是幺元。但是>>=并不完全符合二元运算的定义,所以我们定义新的函数:
>=> :: (a -> m b) -> (b -> m c) -> (a -> m c)
显然,>=>符合这个幺半群里对二元运算的定义。>>=与>=>的关系为对于任意两个函子f, g,有(f x) >>= g等价于(f >=> g) x。
封闭性
对于任意两个自函子f: a -> m b以及g: b -> m c,那么>>= g就是一个m b -> m c的自然变换,将f映射为h: a -> m c,而显然h也是一个自函子,所以满足封闭性。用代码表示就是(>>= g) . f = h。
对于任意两个自函子f: a -> m b以及g: b -> m c,那么f >=> g得到h: a -> m c的自然变换,而显然h也是一个自函子,所以满足封闭性。
结合律
对于任意三个自函子f: a -> m b, g: b -> m c, h: c -> m d,先考虑(f * g) * h的顺序,计算(>>= h) . ((>>= g) . f) = a - > m d。再考虑f * (g * h)的顺序,计算(>>= (>>= h) . g) . f = a - > m d。所以结合律成立。
对于任意三个自函子f: a -> m b, g: b -> m c, h: c -> m d,先考虑(f * g) * h的顺序,计算(f >=> g) >=> h = a - > m d。再考虑f * (g * h)的顺序,计算f >=> (g >=> h) = a - > m d。所以结合律成立。
幺元
首先验证左结合律。取任意自函子f: a -> m b,考虑return * f,计算(>> f) . return = a -> m b = f。左结合律成立。再验证右结合律,考虑f * return,计算(>>= return) . f = a -> m b = f,右结合律成立。
首先验证左结合律。取任意自函子f: a -> m b,考虑return * f,计算return >=> f = a -> m b = f。左结合律成立。再验证右结合律,考虑f * return,计算f >=> return = a -> m b = f,右结合律成立。
综上,我们验证了实现了return和>=>(也就是实现了return和>>=)的Monad实例确实是自函子范畴上的幺半群。这里我们暂时不再证明满足自函子范畴上的幺半群一定是Monad的结论。
Monad有什么用
费尽千辛万苦终于理解了开头一句话的意思,但现在面临的问题是引入Monad究竟给Haskell带来了什么好处呢?无非是解决非纯函数带来的副作用的问题。
那么Monad怎么解决副作用问题呢?
在维基百科的Haskell词条中有如下描述:
它是一门纯函数编程语言,这意味着大体上,Haskell中的函数没有副作用。Haskell用特定的类型来表达副作用,该类型与函数类型相互独立。纯函数可以操作并返回可执行的副作用的类型,但不能够执行它们,只有用于表达副作用的类型才能执行这些副作用,Haskell以此表达其它语言中的非纯函数。
按照我的理解,Haskell对于这些可能有副作用的类型构造了相应的高级类型Higher Order Type,也就是形成了对立于没有副作用的范畴的新范畴。而在这两个范畴之间,通过Monad联系起来。若记无副作用范畴为C1,有副作用范畴为C2。这种联系只有从C1到C2的单向方法以及C2的内部方法,不存在从C2到C1的方法。通过这样的设计来隔离这两个范畴。
还是最初以导致Monad引入的IO类型作为例子说明。
这里的自函子为IO函子,它对Monad类型类的实现如下:
instance Monad IO where
return x = IO x
IO x >>= f = f x
IO是显然的具有副作用的操作。IO类型将这种操作封装为一种类型,return操作提供了从C1到C2的方法,>>=操作提供了C2的内部方法。更准确的说法是道可叨中的说法:return是一种最自然的类型提升,也就是单位函子,>>=是一种首先的类型下降,但是确保了结果还是在IO类型的范畴当中。
通过Monad的机制,确保了有副作用的范畴中的执行始终停留在有副作用的范畴中,不会影响原来的类型。
最后我想补充一点,Monad是如何解决执行顺序对于有副作用函数的影响。我的理解是>>=实际上类似于shell中的|,它构造了一种管道,使得函数的执行是有顺序的。但是这与幺半群的结合律是否矛盾呢?并不矛盾。因为例如对于m >>= f >>= g ...中除了第一个参数,后续的部分只是明确了执行的过程,并没有实际的输入执行,必须等到m进入管道后才能真正开始计算结果。所以与结合律并不矛盾。
引用道可叨的一张图,希望能帮助理解。
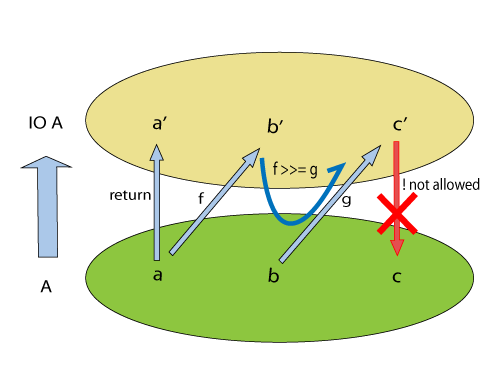
程序示例
有道寒假实践题目是调查自己的家族图谱。如果我们构想了一个数据结构存储了所有收集到的关于一个族谱的信息。从其中某一个人出发,要获得与他相关的任意一个人,可以经过一步或者多步如下的关系获得:父亲(father),母亲(mother),丈夫或妻子(husbandOrWife),长子或长女(eldestChild),最大的弟弟或妹妹(nextChild)
于是我构造了如下的例子:
data Person = Person String
deriving Show
father :: Person -> Maybe Person
mother :: Person -> Maybe Person
husbandOrWife :: Person -> Maybe Person
eldestChild :: Person -> Maybe Person
nextChild :: Person -> Maybe Person
这里我们用了Monad类型的Maybe。它给我们带来了什么好处呢?由于不是每一个人都拥有上述五种关系的人,或者由于族谱的缺失,数据不一定完整。所以有可能经过上述某一步操作,没有期望的结果。如果我们采用对函数结果进行判断,则代码会演变成类似If...else...结构冗长的嵌套。Maybe由于实现了Monad类型,通过>>=我们可以正常地寻找某人,中间过程不用加以判断,如果某一步出现找不到,则结果会变为Nothing(不是说他不是东西。。。)。简直太有爱了!
从范畴角度来看,由于Maybe类型存在例外的Nothing的情况,所以Monad使得涉及Maybe的操作被限制在Maybe对应的范畴内,从而使程序设计变得容易。